case, caseZ, caseX …..!!!! it use to be very confusing for me to differentiate between these three and i use to think that whats the need of other two guy (caseZ and caseX). I hope this article will help you to understand it in better way.
The common practice is to use casez statement in RTL coding. Use of casex is strongly discouraged. Now we will discuss whether casex is such a bad construct. Before we start let me say, all case statements are synthesizable.
If someone is required to tell the differences between case, casez, casex constructs in
verilog, the answer will be the pretty familiar one:
casez treats 'z' as dont care.
casex treats 'z' & 'x' as dont care.
case treats 'z' & 'x' as it is.
Now lets go further and unearth the differences between them.
A common misconception is '?' does mean a don’t care, but it does not. It is just an another representation of high impedence 'z'.
Ex:
case (sel)
00: mux_out = mux_in[0];
01: mux_out = mux_in[1];
1?: mux_out = mux_in[2];
default: mux_out = mux_in[3];
endcase
In the above case statement if the intention is to match case item 3 to either 10 or 11 then the code is absolutely wrong, because '?' doesnot mean a dont care. The actual case item written is 1z.
Case statement:
Case statement treats x & z as it is. So a case expression containing x or z will only match a case item containing x or z at the corresponding bit positions. If no case item matches then default item is executed. Its more like pattern matching. Any pattern formed from the symbol set {0,1,x,z} will match its clone only.
Ex:
case (sel)
00: y = a;
01: y = b;
x0: y = c;
1x: y = d;
z0: y = e;
1?: y = f;
default: y = g;
endcase
Result:
sel y case item
00 a 00
11 g default
xx g default
x0 c x0
1z f 1?
z1 g default
Note that when sel is 11, y is not assigned f, but is assigned the default value g.
Casez statement:
Casez statement treats z as dont care. It mean what it sounds, 'don’t care' (dont care whether the bit is 0,1 or even x i.e, match z(?) to 0 or 1 or x or z).
Ex:
casez (sel)
00: y = a;
01: y = b;
x0: y = c;
1x: y = d;
z0: y = e;
1?: y = f;
default: y = g;
endcase
Result:
sel y case item
00 a 00
11 f 1?
xx g default
x0 c x0 (would have matched with z0(item 5) if item 3
is not present.)
1z d 1x (would have matched with z0(item 5) &
1? (item 6) also.)
z1 b 01 (would have matched with 1?(item 6) also.)
The fact that x matches with z in casez gives the illusion 'x is being treated as a dont care in casez'. What is exactly happening is z, the dont care, is being matched to x. This will be more clear if you admire the fact 'x will not be matched to 1 or 0 in casez'(but will match z).
The point we dicussed at the beginning that ? is not dont care is worth an explanation here. ? is dont care only when used in casez, elsewhere it is nothing but z.
Casex statement:
Casex statement treats x and z as dont cares. x will be matched to 0 or 1 or z or x and z will be matched to 0 or 1 or x or z.
Ex:
casex (sel)
00: y = a;
01: y = b;
x0: y = c;
1x: y = d;
z0: y = e;
1?: y = f;
default: y = g;
endcase
Result:
sel y case item
00 a 00
11 d 1x (would have matched with 1? also)
xx a 00 (would have matched with 1? also)
x0 a 00 (would have matched with all items except 01)
1z c x0 (would have matched with all items except
00,01)
z1 b 01 (would have matched with 1x, 1? also)
The summary of the discussion so far can be put up as follows:
Statement Expression contains Item contains Result
Case Binary Binary Match
Binary x Don’t match
Binary ? (z) Don’t match
x Binary Don’t match
x x Match
x ? (z) Don’t match
z (?) Binary Don’t match
z (?) x Don’t match
z (?) ? (z) Match
Casez Binary Binary Match
Binary x Don’t match
Binary ? (z) Match
x Binary Don’t match
x x Match
x ? (z) Match
z (?) Binary Match
z (?) x Match
z (?) ? (z) Match
Casex Binary Binary Match
Binary x Match
Binary ? (z) Match
x Binary Match
x x Match
x ? (z) Match
z (?) Binary Match
z (?) x Match
z (?) ? (z) Match
We have been discussing the simulations aspects, now we will discuss synthesis aspects of these statements.
Ex: case (sel)
00: mux_out = mux_in[0];
01: mux_out = mux_in[1];
1?: mux_out = mux_in[2];
default: mux_out = mux_in[3];
endcase
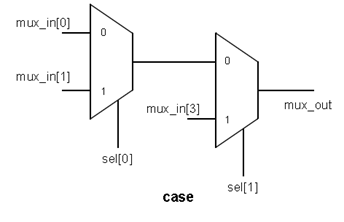
The outputs after synthesis for different case statements of the same code is shown below:
Now let the case item 3 be changed to 1x.
Ex: case (sel)
00: mux_out = mux_in[0];
01: mux_out = mux_in[1];
1x: mux_out = mux_in[2];
default: mux_out = mux_in[3];
endcase
The outputs of synthesis will look like:
We can have the following deductions by comparing the two sets of outputs.
1. Case statement will not consider for synthesis, the items containing x or z.
2. Casez and Casex will give the same output after synthesis, treating both x, z in case items as dont cares.(seems against the nature of casez ?)
If both casez and casex give the same netlist, then why was I adviced to use casez only in RTL design? The immediate answer would be because of synthesis-simulation mismatch. If I use casez then, will there be no mismatches? The painful fact is tha t there will be mismatches.
Normally in any RTL designed to be synthesized, no case item will be expected, rather desired to be x (as no such unknown state will be present on the chip). So we wont have any case item carrying x (as shown in the below example where only 0,1,?(z) is used).
Ex: casez (sel)
00: mux_out = mux_in[0];
01: mux_out = mux_in[1];
1?: mux_out = mux_in[2];
default: mux_out = mux_in[3];
endcase
Result:
casez casex
sel Pre-synthesis Post-synthesis Pre-synthesis Post-synthesis
xx mux_in[3] x mux_in[0] x
1x mux_in[2] mux_in[2] mux_in[2] mux_in[2]
0x mux_in[3] x mux_in[0] x
zz mux_in[0] x mux_in[0] x
1z mux_in[2] mux_in[2] mux_in[2] mux_in[2]
0z mux_in[0] x mux_in[0] x
Note:
1.Binary combinations of sel signal are not considered as its obvious that no mismatch can occur for them.
2.Post-synthesis results of casez and casex match because both have the same netlist.
If we observe the pre and post synthesis results for casez, certainly there are some mismatches. For casex also there are some mismatches. In some mismatches(when sel is xx,0x), the pre-synthesis result of casez is different from pre-synthesis result of casex, but during the match conditions(when sel is 1x,1z) both casez and casex have the same pre-synthesis results.
Another interesting, very important observation is that when ever there is a mismatch, post-synthesis result will become x. This is such a crucial observation that it will make us reach the conclusion that we can use either casez or casex, which ever we wish as opposed to the common myth to use casez only. This is explained below in a detailed manner.
During RTL simulation if sel becomes xx, casez executes default statement(which is the intended behaviour) but casex executes case item1(which is not the intended behaviour), clearly a mismatch. In netlist simulation both casez and casex results will become x, making the RTL simulation mismatch between casez and casex trivial.
In all the cases where the netlist simulation result is not x, the RTL simulation results of casez and casex will match.From this behaviour we can conclude that casex can be used as freely as casez is being used in designs.
The reason why we prefer casez(casex) to case stament is that casez(casex) has the ability to represent dont cares.
Ex: casez (sel)
000: y = a;
001: y = b;
01?: y = c;
1??: y = d;
endcase
The same logic if we implement using case statement it will be like:
case (sel)
000: y = a;
001: y = b;
010,011: y = c;
100,101,110,111: y = d;
endcase
The number of values for a single case item may increase if the case expression size increases, resulting in the loss of readability and also it will make the coding difficult. Also do remember that the synthesized netlist will be different from that of casez (casex), if the case items contain x or z(?).
Summary:
1. We can’t put ?(meaning a z) or x in case item of a case statement as synthesis tool
wont consider that case item for synthesis.
2. casez and casex will result in the same netlist.
3. casez is preferred to case, only because it has the ability to represent dont cares.
4. The most important conclusion is that casex can also be used as freely as the casez
statement.
5. If you visualize a design in terms of gates(muxes) and then derive the case items for
that logic, then they can be put inside a casez or casex statement (both will give the same
results).