The Story Of Electronics

Here is a great video - The Story of Electronics by The Story of Stuff Project. It outlines how electronic manufacturers are "Designing for the dump".
As consumers we must pressure these companies to take ownership of electronics from cradle to grave, and change from "dump designers" to sustainable designers.
This is where Design For Sustainability Software (DFS) can be integral to changing the disposable mindset of these organizations.

Designed for the Dump
Many electronic products are designed for the dump. They have short-life spans, or become obsolete quickly. They are often expensive to repair, and sometimes it’s difficult to find parts. Many consumer-grade electronics products are cheaper to replace than to fix even if you can find someone to fix it.  Because they are designed using  many hazardous compounds, recycling these products involves processing toxic material streams, which is never 100% safe.

Some of the problematic toxic materials that must be removed before recycling are lead in cathode ray tube (CRT) TV monitors and mercury lamps in LCD screens, as well as PVC, flame retardants, and other toxic additives in plastic components.

Designed to Last
Before electronics companies can make the claim that they are green and sustainable, they must shift away from producing “disposable” products designed with a limited lifespan (planned obsolescence) and towards products that are designed to last. Instead of purchasing products with high failure rates and the need for frequent replacement, we should be able to choose long-living, upgradeable goods that have long warranties and can be efficiently repaired and recycled.

Difference between DDR3 and DDR4 RAM

DDR4 is the next evolution in DRAM, bringing even higher performance and more robust control features while improving energy economy for enterprise, micro-server, tablet, and ultrathin client applications. The following table compares some of the key feature differences between DDR3 and DDR4.

Feature/Option	DDR3	DDR4	DDR4 Advantage
Voltage (core and I/O)	1.5V	1.2V	Reduces memory power demand
VREF inputs	2 – DQs and CMD/ADDR	1 – CMD/ADDR	VREFDQ now internal
Low voltage standard	Yes  (DDR3L at 1.35V)	Anticipated  (likely 1.05V)	Memory power reductions
Data rate (Mb/s)	800, 1066, 1333, 1600, 1866, 2133	1600, 1866, 2133, 2400, 2667, 3200	Migration to higher‐speed I/O
Densities	512Mb–8Gb	2Gb–16Gb	Better enablement for large-capacity memory subsystems
Internal banks	8	16	More banks
Bank groups (BG)	0	4	Faster burst accesses
tCK – DLL enabled	300 MHz to 800 MHz	667 MHz to 1.6 GHz	Higher data rates
tCK – DLL disabled	10 MHz to 125 MHz (optional)	Undefined to 125 MHz	DLL-off now fully supported
Read latency	AL + CL	AL + CL	Expanded values
Write latency	AL + CWL	AL + CWL	Expanded values
DQ driver (ALT)	40Ω	48Ω	Optimized for PtP (point-to-point) applications
DQ bus	SSTL15	POD12	Mitigate I/O noise and power
RTT values (in Ω)	120, 60, 40, 30, 20	240, 120, 80, 60, 48, 40, 34	Support higher data rates
RTT not allowed	READ bursts	Disables during READ bursts	Ease-of-use
ODT modes	Nominal, dynamic	Nominal, dynamic, park	Additional control mode; supports OTF value change
ODT control	ODT signaling required	ODT signaling not required	Ease of ODT control, allows non-ODT routing on PtP applications
Multipurpose register (MPR)	Four registers – 1 defined, 3 RFU	Four registers – 3 defined, 1 RFU	Provides additional specialty readout

Myths of Verilog Case Statement

case, caseZ, caseX …..!!!! it use to be very confusing for me to differentiate between these three and i use to think that whats the need of other two guy (caseZ and caseX). I hope this article will help you to understand it in better way.
 
The common practice is to use casez statement in RTL coding. Use of casex is strongly discouraged. Now we will discuss whether casex is such a bad construct. Before we start let me say, all case statements are synthesizable.

If someone is required to tell the differences between case, casez, casex constructs in
verilog, the answer will be the pretty familiar one:

casez treats 'z' as dont care.
casex treats 'z' & 'x' as dont care.
case treats 'z' & 'x' as it is.

Now lets go further and unearth the differences between them.

A common misconception is '?' does mean a don’t care, but it does not. It is just an another representation of high impedence 'z'.

Ex:
case (sel)
00: mux_out = mux_in[0];
01: mux_out = mux_in[1];
1?: mux_out = mux_in[2];
default: mux_out = mux_in[3];
endcase

In the above case statement if the intention is to match case item 3 to either 10 or 11 then the code is absolutely wrong, because '?' doesnot mean a dont care. The actual case item written is 1z.

Case statement:
Case statement treats x & z as it is. So a case expression containing x or z will only match a case item containing x or z at the corresponding bit positions. If no case item matches then default item is executed. Its more like pattern matching. Any pattern formed from the symbol set {0,1,x,z} will match its clone only.
Ex:
case (sel)
00: y = a;
01: y = b;
x0: y = c;
1x: y = d;
z0: y = e;
1?: y = f;
default: y = g;
endcase

Result:
sel           y           case item
00           a           00
11           g           default
xx           g           default
x0           c           x0
1z           f           1?
z1           g           default
Note that when sel is 11, y is not assigned f, but is assigned the default value g.

Casez statement:
Casez statement treats z as dont care. It mean what it sounds, 'don’t care' (dont care whether the bit is 0,1 or even x i.e, match z(?) to 0 or 1 or x or z).

Ex:
casez (sel)
00: y = a;
01: y = b;
x0: y = c;
1x: y = d;
z0: y = e;
1?: y = f;
default: y = g;
endcase

Result:
sel           y           case item
00           a           00
11           f           1?
xx           g           default
x0           c           x0 (would have matched with z0(item 5) if item 3
                           is not present.)
1z           d           1x (would have matched with z0(item 5) &
                           1? (item 6) also.)
z1           b           01 (would have matched with 1?(item 6) also.)

The fact that x matches with z in casez gives the illusion 'x is being treated as a dont care in casez'. What is exactly happening is z, the dont care, is being matched to x. This will be more clear if you admire the fact 'x will not be matched to 1 or 0 in casez'(but will match z).

The point we dicussed at the beginning that ? is not dont care is worth an explanation here. ? is dont care only when used in casez, elsewhere it is nothing but z.

Casex statement:
Casex statement treats x and z as dont cares. x will be matched to 0 or 1 or z or x and z will be matched to 0 or 1 or x or z.

Ex:
casex (sel)
00: y = a;
01: y = b;
x0: y = c;
1x: y = d;
z0: y = e;
1?: y = f;
default: y = g;
endcase

Result:
sel           y           case item
00           a           00
11           d           1x (would have matched with 1? also)
xx           a           00 (would have matched with 1? also)
x0           a           00 (would have matched with all items except 01)
1z           c           x0 (would have matched with all items except
                           00,01)
z1           b           01 (would have matched with 1x, 1? also)

The summary of the discussion so far can be put up as follows:
Statement        Expression         contains           Item contains Result
Case                Binary                Binary              Match
                       Binary                x                     Don’t match
                       Binary                ? (z)                 Don’t match
                       x                       Binary              Don’t match
                       x                       x                     Match
                       x                       ? (z)                 Don’t match
                       z (?)                  Binary               Don’t match
                       z (?)                  x                      Don’t match
                       z (?)                  ? (z)                 Match
Casez              Binary               Binary               Match
                       Binary               x                      Don’t match
                       Binary               ? (z)                  Match
                       x                      Binary               Don’t match
                       x                      x                      Match
                       x                      ? (z)                 Match
                       z (?)                 Binary               Match
                       z (?)                 x                      Match
                       z (?)                 ? (z)                 Match
Casex              Binary              Binary               Match
                      Binary               x                      Match
                      Binary               ? (z)                 Match
                      x                     Binary                Match
                      x                     x                       Match
                      x                     ? (z)                   Match
                      z (?)                Binary                 Match
                      z (?)                x                        Match
                      z (?)                ? (z)                   Match

We have been discussing the simulations aspects, now we will discuss synthesis aspects of these statements.

Ex: case (sel)
00: mux_out = mux_in[0];
01: mux_out = mux_in[1];
1?: mux_out = mux_in[2];
default: mux_out = mux_in[3];
endcase

The outputs after synthesis for different case statements of the same code is shown below:

Now let the case item 3 be changed to 1x.

Ex: case (sel)
00: mux_out = mux_in[0];
01: mux_out = mux_in[1];
1x: mux_out = mux_in[2];
default: mux_out = mux_in[3];
endcase

The outputs of synthesis will look like:

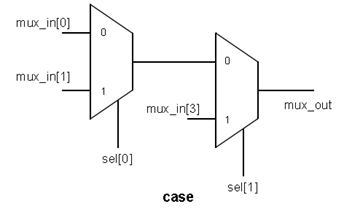
We can have the following deductions by comparing the two sets of outputs.
1. Case statement will not consider for synthesis, the items containing x or z.
2. Casez and Casex will give the same output after synthesis, treating both x, z in case items as dont cares.(seems against the nature of casez ?)

If both casez and casex give the same netlist, then why was I adviced to use casez only in RTL design? The immediate answer would be because of synthesis-simulation mismatch. If I use casez then, will there be no mismatches? The painful fact is tha t there will be mismatches.

Normally in any RTL designed to be synthesized, no case item will be expected, rather desired to be x (as no such unknown state will be present on the chip). So we wont have any case item carrying x (as shown in the below example where only 0,1,?(z) is used).

Ex: casez (sel)
00: mux_out = mux_in[0];
01: mux_out = mux_in[1];
1?: mux_out = mux_in[2];
default: mux_out = mux_in[3];
endcase

Result:
                            casez                                           casex
sel      Pre-synthesis      Post-synthesis      Pre-synthesis      Post-synthesis
xx      mux_in[3]           x                           mux_in[0]            x
1x      mux_in[2]           mux_in[2]              mux_in[2]            mux_in[2]
0x      mux_in[3]           x                           mux_in[0]            x
zz      mux_in[0]           x                            mux_in[0]            x
1z      mux_in[2]           mux_in[2]              mux_in[2]            mux_in[2]
0z      mux_in[0]           x                           mux_in[0]             x

Note:
1.Binary combinations of sel signal are not considered as its obvious that no mismatch can occur for them.
2.Post-synthesis results of casez and casex match because both have the same netlist.

If we observe the pre and post synthesis results for casez, certainly there are some mismatches. For casex also there are some mismatches. In some mismatches(when sel is xx,0x), the pre-synthesis result of casez is different from pre-synthesis result of casex, but during the match conditions(when sel is 1x,1z) both casez and casex have the same pre-synthesis results.
Another interesting, very important observation is that when ever there is a mismatch, post-synthesis result will become x. This is such a crucial observation that it will make us reach the conclusion that we can use either casez or casex, which ever we wish as opposed to the common myth to use casez only. This is explained below in a detailed manner.

During RTL simulation if sel becomes xx, casez executes default statement(which is the intended behaviour) but casex executes case item1(which is not the intended behaviour), clearly a mismatch. In netlist simulation both casez and casex results will become x, making the RTL simulation mismatch between casez and casex trivial.

In all the cases where the netlist simulation result is not x, the RTL simulation results of casez and casex will match.From this behaviour we can conclude that casex can be used as freely as casez is being used in designs.

The reason why we prefer casez(casex) to case stament is that casez(casex) has the ability to represent dont cares.

Ex: casez (sel)
000: y = a;
001: y = b;
01?: y = c;
1??: y = d;
endcase
 

The same logic if we implement using case statement it will be like:

case (sel)
000: y = a;
001: y = b;
010,011: y = c;
100,101,110,111: y = d;
endcase

The number of values for a single case item may increase if the case expression size increases, resulting in the loss of readability and also it will make the coding difficult. Also do remember that the synthesized netlist will be different from that of casez (casex), if the case items contain x or z(?).

Summary:
1. We can’t put ?(meaning a z) or x in case item of a case statement as synthesis tool
wont consider that case item for synthesis.
2. casez and casex will result in the same netlist.
3. casez is preferred to case, only because it has the ability to represent dont cares.
4. The most important conclusion is that casex can also be used as freely as the casez
statement.
5. If you visualize a design in terms of gates(muxes) and then derive the case items for
that logic, then they can be put inside a casez or casex statement (both will give the same
results).

SystemVerilog Data Types

SystemVerilog offers many improved data structures compared with Verilog. Some of these were created for designers but are also useful for testbenches. In this post of SystemVerilog Tutorial you will learn about the data structures most useful for verification.

SystemVerilog introduces new data types with the following benefits.

1. Two-state: better performance, reduced memory usage.
2. Queues, dynamic and associative arrays and automatic storage: reduced memory usage, built-in support for searching and sorting
3. Unions and packed structures: allows multiple views of the same data
4. Classes and structures: support for abstract data structures
5. Strings: built-in string support
6. Enumerated types: code is easier to write and understand

Learn More about Systemverilog Data types :

1. Built-In Data Types
2. Enumerated Types
3. Constants
4. Strings
5. Net Types
6. Fixed Size Arrays
7. Dynamic Arrays
8. Associative Arrays
9. Queues
10. Linked Lists
11. Array Methods
12. Comparison Of Arrays

SystemVerilog Language Reference Manual (LRM)

IEEE Standard 1800™ SystemVerilog is the industry's unified hardware description and verification language (HDVL) standard. SystemVerilog is a significant evolution of the traditional Verilog hardware description language. Its use dramatically improves productivity in the development of large-gate-count, IP-based, and bus-intensive chips. SystemVerilog is targeted primarily at the chip implementation and verification flows, with powerful links to the system-level design flow. SystemVerilog has been adopted by hundreds of semiconductor design companies and is supported by more than 75 EDA, IP, and training solutions providers worldwide.

IEEE Standard 1800™-2012 SystemVerilog LRM can be downloaded through the IEEE-SA and industry support, in PDF format, at no charge from below link.

DOWNLOAD SYSTEM VERILOG LRM PDF

8-bit Micro Processor

This is 8-bit microprocessor with 5 instructions. It is based on 8080 architecture. This architecture called SAP for Simple-As-Possible computer. It very useful design which introduces most of the basic and fundamental ideas behind computer operation.

This design could be used for instruction classes for undergraduate classes or specific VHDL classes. This processor is based on the 8080 architecture, therefore, it could be upgraded step by step to integrate further facilities. It is very exciting challenge for the students to do so. Further, they could think about building complete system, i.e. integrating and I/O peripherals to the processor.

The design is proven for ASIC and FPGA. It was implemented using Xilinx FPGA Spartan-3E starter kit. A full documentation for the code and the used resources are attached within the project.

For project details please write to us on info@vlsiencyclopedia.com

Get free daily email updates!

Follow us!

Floating Point Adder and Multiplier

The FP Adder is a single-precision, IEEE-754 compliant, signed adder/substractor. It includes both single-cycle and 6-stage pipelined designs. The design is fully synthesizable and has been tested in a Xilinx Virtex-II XC2V3000 FPGA, occupying 385 CLBs and with a theoretical maximum operating frequency of 6MHz for the single-cycle design and 87MHz for the pipelined design. The design was tested at 33MHz.

The FP Multiplier is a single-precision, IEEE-754 compliant, signed multiplier. It includes both single-cycle and 4-stage pipelined designs. The design is fully synthesizable and has been tested in a Xilinx Virtex-II XC2V3000 FPGA, occupying 119 CLBs and with a theoretical maximum operating frequency of 8MHz for the single-cycle design and 90MHz for the pipelined design. The design was tested at 33MHz.

Features

- IEEE-754 compliant
- 32 bits, single precision
- Works with normalized and un-normalized numbers
- Simple block design, good for FP arithmetic learning
- Adder
- 385 CLBs
- 87 MHz, 6-stage pipelined
- Multiplier
- 119 CLBs
- 90 MHz, 4-stage pipelined