Understanding Logic gates at transistor level : Not Gate

Today we will talk about some basics of digital logic gates. It's about using the transistor for the construction of logic gates. Transistors are used in the construction of logic gates as they act as fast switches. 

When the base-emitter diode is turned on enough to be driven into saturation, the collector voltage with respect to the emitter may be near zero and can be used to construct gates for the TTL logic family. Let's start with simple NOT gate.

1. Not Gate using transistor

NOT gates are single-input devices which have an output level that is normally at logic level “1” and goes “LOW” to a logic level “0” when its single input is at logic level “1”, in other words, it “inverts” (complements) its input signal. The output from a NOT gate only returns “HIGH” again when its input is at logic level “0” giving us the Boolean expression A = Q.

The input of the NOT Gate is connected at the base of the transistor and the output is taken from the collector. The transistor here acts as the switch so when the voltage is applied at the base of the transistor the transistor starts conducting and shorts the output to the ground similarly when no voltage is applied at the input the output is connected to the Vcc as shown thus in this way the circuit implements the NOT function.

Creating a simple FPGA Project with Xilinx ISE

We would like to write this post for our friends who wants to create a simple FPGA Project with Xilinx ISE. 

Software

Xilinx ISE as a software package containing a graphical IDE, design entry tools, a simulator, a synthesizer (XST) and implementation tools. Limited version of Xilinx ISE (WebPack) can be downloaded for free from the Xilinx website.

It is not mandatory to use Xilinx software for all tasks (for example, synthesis can be done with Synplify, simulation - with Modelsim etc.), but it is the easier option to start off.

The information in this article applies to Xilinx ISE version 9.2.03i, but other versions (since 8.x) shouldn't be very different. If your version is older than 8.x, you'd better upgrade.

Creating a project

To create a project, start a Project Navigator and select File->New Project. You will be asked for project name and folder. Leave "top-level source type" as HDL.

Now we should choose a target device (we will use a Spartan-3A xc3s50a device as an example) as well as set up some other options:

The Project Navigator window contains a sidebar, which is on the left side by default. The upper part of this sidebar lists all project files, and the lower part lists tasks that are applicable for the file selected in the upper part.

Design Entry

Now, let's add a new source file to our project. We'll start from a simple 8-bit counter, which adds 1 to its value every clock cycle. This counter will have the following ports:

• CLK - input clock signal;
• CLR - input asynchronous clear signal (set counter value to 0);
• DOUT - output counter value (8-bit bus).

We'll define our counter as a VHDL module. VHDL language will be covered in more details in further chapters.

To create a new source file, choose "Create New Source" task and select "VHDL module" source type. The name of our module will becounter.vhd. Then you will be asked which module to associate the testbench with; choose counter.

Let's write the following code in counter.vhd:

library IEEE;
use IEEE.STD_LOGIC_1164.ALL;
use IEEE.STD_LOGIC_ARITH.ALL;
use IEEE.STD_LOGIC_UNSIGNED.ALL;

entity counter is
    Port ( CLK : in  STD_LOGIC;
           CLR : in  STD_LOGIC;
           DOUT : out  STD_LOGIC_VECTOR (7 downto 0));
end counter;

architecture Behavioral of counter is

signal val: std_logic_vector(7 downto 0);

begin

process (CLK,CLR) is
begin
    if CLR='1' then
        val<="00000000";
    elsif rising_edge(CLK) then
        val<=val+1;
    end if;
end process;

DOUT<=val;

end Behavioral;

ISE inserted library and ports declarations automatically, we only need to write an essential part of VHDL description (inside thearchitecture block).

To check VHDL syntax, select "Synthesize - XST => Check Syntax" task for our module.

Simulation

In order to check that our code works as intended, we need to define input signals and check that output signals are correct. It can be done by creating a testbench.

To create a testbench for our counter, select "Create New Source" task, choose "VHDL Test Bench" module type and name it, for instance, counter_tb.vhd.

VHDL test bench is written in VHDL, just like a hardware device description. The difference is that a testbench can utilize some additional language constructs that aren't synthesizable and therefore cannot be used in real hardware (for example wait statements for delay definition).

In order for testbench file to be visible, choose "Behavioral Simulation" in the combobox in the upper part of the sidebar.

ISE automatically generates most of the testbench code, we need only to add our "stimulus":

LIBRARY ieee;
USE ieee.std_logic_1164.ALL;
USE ieee.std_logic_unsigned.all;
USE ieee.numeric_std.ALL;

ENTITY counter_tb_vhd IS
END counter_tb_vhd;

ARCHITECTURE behavior OF counter_tb_vhd IS

    -- Component Declaration for the Unit Under Test (UUT)
    COMPONENT counter
    PORT(
        CLK : IN std_logic;
        CLR : IN std_logic;         
        DOUT : OUT std_logic_vector(7 downto 0)
        );
    END COMPONENT;

    --Inputs
    SIGNAL CLK :  std_logic := '0';
    SIGNAL CLR :  std_logic := '0';

    --Outputs
    SIGNAL DOUT :  std_logic_vector(7 downto 0);

BEGIN

    -- Instantiate the Unit Under Test (UUT)
    uut: counter PORT MAP(
        CLK => CLK,
        CLR => CLR,
        DOUT => DOUT
    );
    -- Clock generation   
    process is
    begin
        CLK<='1';
        wait for 5 ns;
        CLK<='0';
        wait for 5 ns;
    end process;

    tb : PROCESS
    BEGIN

        CLR<='1';
        wait for 100 ns;

        CLR<='0';

        wait; -- will wait forever
    END PROCESS;

END;

We have added the clock generation process (which generates 100MHz frequency clock) and reset stimulus.

Now select a test bench source file and apply "Xilinx ISE Simulator => Simulate Behavioral Model" task. We should get something like this:

It can be seen that our counter works properly.

Synthesis

The next step is to convert our VHDL code into a gate-level netlist (represented in the terms of the UNISIM component library, which contains basic primitives). This process is called "synthesis". By default Xilinx ISE uses built-in synthesizer XST (Xilinx Synthesis Technology).

In order to run synthesis, one should select "Synthesis/Implementation" in the combobox in the upper part of the sidebar, select a top-level module and apply a "Synthesize - XST" task. If the code is correct, there shouldn't be any pproblems during the synthesis.

Synthesizer report contains many useful information. There is a maximum frequency estimate in the "timing summary" chapter. One should also pay attention to warnings since they can indicate hidden problems.

After a successful synthesis one can run "View RTL Schematic" task (RTL stands for register transfer level) to view a gate-level schematic produced by a synthesizer:

Notice that an RTL schematic in question contains only one primitive: a counter, which is directly an element from the UNISIM library.

Synthesizer output is stored in NGC format.

Implementation

Implementation design flow

1. Translate - convert NGC netlist (represented in the terms of the UNISIM library) to NGD netlist (represented in the terms of the SIMPRIM library). The difference between these libraries is that UNISIM is intended for behavioral simulation, and SIMPRIM is a physically-oriented library (containing information about delays etc.) This conversion is performed by the program NGDBUILD and is rather straightforward. The main reason for it to be included is to convert netlist generated by different design entry methods (e.g. schematic entry, different synthesizers etc.) into one unified format.
2. Map is a process of mapping the NGD netlist onto the specific resources of the particular device (logic cells, RAM modules, etc.) This operation is performed by the MAP program with resutls being stored in NCD format. For Virtex-5 MAP also does placement (see below).
3. Place and route - as can be inferred from its name, this stage is responsible for the layout. It performs placement (logic resources distribution) and routing (connectivity resources distribution). Place and route is performed by a PAR program. For Virtex-5 devices, though, placement is performed by MAP program (and routing still by PAR program). The output of PAR is stored, again, in NCD format.

Implementation Constraints

Constraints are very important during the implementation. They define pin assignments, clocking requirements and other parameters influencing implementation. Constraints are stored in UCF format (user constraints file).

In order to add constraints one need to add a new source (using "Create New Source" task) and choose "Implementation constraints file" source type. UCF file is a text file that can be directly edited by a user, however, simple consraints can be defined with graphical interface.

When a constraints file is selected in the upper part of the sidebar, the specific tasks become available. These include "Create Timing Constraints" and "Assign Package Pins".

For example, if we specify a frequency requirement on CLK as 100 MHz, the corresponding section of the constraints file will be:

NET "CLK" TNM_NET = CLK;
TIMESPEC TS_CLK = PERIOD "CLK" 100 MHz;

When timing requirements are specified in the constraints file, the implementation tools will strive to meet them (and report an error in the case it can't be met).

Package pins constraints must also be set (according to the board layout).

MAP program converts UCF constraints to the PCF format which is later used by PAR.

There are also synthesis constraints stored in XCF files. They are used rarely and shouldn't be confused with implementation constraints.

Programming file generation

After placement and routing, a file should be generated that will be loaded into the FPGA device to program it. This task is performed by a BITGEN program.

The programming file has .bit extension.

The programming file is loaded to the FPGA using iMPACT.

Get free daily email updates!

Follow us!

Tips for Implementing State Machine

At a low level of abstraction, a protocol is often most easily understood as a state machine. Design criteria can also easily be expressed in terms of desirable or undesirable protocol states and state transitions. In a way, the protocol state symbolizes the assumptions that each process in the system makes about the others. It defines what actions a process is allowed to take, which events it expects to happen, and how it will respond to those events.

The Xcell Journel Issue 81 gives some important tips on implementing state machines in your FPGA

Link to Xcell Journel issue 81

Get free daily email updates!

Follow us!

Combinational Loop in Design

Combinational loops are logical structures that contain no synchronous feedback element. This kind of loops cause stability and reliability problemas,  as we will see in this article, violating the synchronous principles by making feedback with no register in the loop.

WHY? HOW? IS GENERATED A COMBINATIONAL LOOP? 

Basically, a combinational loop es implemented in hardware (gates) when in the written VHDL code describing combinational logic a signal that is in the left side of an assignment statement (that is, to the left of the <= symbol) it also is on the expression at the right side of the signal assignment statement (right of <=). For example the following lines of code generate a combinational loop, as long as they are written in a combinational process or in a concurrent signal assignment statement.

1 acc <= acc + data;
2
3 Z <= Z nand B;
4
5 cnt <= cnt + 1;

However, it's important to point out that if these same statements are written in a clocked process, each of them will generate the respective sequential logic. This is due to the fact that the signal assignment statement in clocked process will generate a register for the assigned signal, therefore the loop will be registered in this case, therefore no combinational loop is generated.

HARDWARE

The following figure shows a diagram of a combinational loop. 

As it is shown in the figure, the combinational logic output is fedbacked to the same combinational logic without any register in the loop. The logic between the first input an the last output can be made up of one or several levels of combinational logic. It can also have different signals coming in and coming out of that piece of logic, but at least one of the signal is going back (feedback) to the first logic level, as it can be seen in the following figure.

This kind of logic circuit usually is not desired, no wanted to be implemented. Hence, when the synthesis tool finds out about this combinational loop generates a warning message. 

Here is an example of VHDL code that generate a combinational loop when is implemented.

1 library ieee;
2 use ieee.std_logic_1164.all;
3
4 entity lazo_comb is
5 port(
6     a: in std_logic;
7     z: out std_logic);
8 end lazo_comb;
9
10 architecture beh of lazo_comb is
11
12 signal y: std_logic;
13
14 begin
15     z <= y;
16
17 process(a,y)
18 begin
19     y <= y nand a;
20 end process;
21
22 end beh;

The synthesis tool, Synplify in this case, generates the following warning regarding the combinational loop. 

The warning message "found combinational loop at 'y'" means that the signal 'y' is feed-backed to the input of the combinational logic without any register in the loop. This loop can be easily found when seeing the RTL view of the synthesized system, as it can be seen in the following figure. 

SIMULATION

The simulation of the system (very simple system) is shown in the following figure. 

The ModelSim windows details a lot of information that deserve a detailed analysis. First of all, the top window plots the waveforms of the signals from the described system, whose main expression is in the line 24 of the middle window. The bottom window, Transcript window, generates an error message, saying that the limit of iterations has been reached at 50ns and no stable value has been gotten. In other words, this mean that the system has began to oscillated and remained oscillating. The maximum number of iterations is configurable in ModelSim (Simulate->Runtime Options); as it's in most simulators. By default this value is set to 5000. Another important piece of information can be found in the bottom of the waveform window. There you can read that the number of Delta reached 5000, which is exactly the number maximum of iterations set in the runtime options, and even after that amount of deltas the system is not stable.

Why this simple logic is oscillating?
Well, analyzing the true table of the nand gate, while one of the input is stuck at '0', the output will be always '1'. That is happening in the simulation shown above. Whereas, when the input (signal a in the simulation) tries to change to '1', due to the fact the other input is still at '1' the output change to '0', then since the feedback input is '0', the output should go to '1', then that '1' is going back with the other input at '1', the output will go to '0' again, and so on...This is what is called an "unstable combinational loop". This kind of loop should NEVER be used in a real design.

Other point to bring out on this example is the importance of simulating a system. Assuming that we configured the FPGA without any simulation, based on the fact that the synthesis tool just gave us a 'warning'), we'd see an no stable output, spending some time (maybe a lot of time) trying to find out why the output is not stable. Conversely, by doing the simulation the problem would appear at first shot.

CODE STYLE

In designs with a large, very large, amount of code lines it is very easy to make mistakes and generate a combinational loop with no intention (as it can be seen in the example above). So, follow certain order when writting the code, trying to maintain a certain flow of data. Also, take a close look at the warnings generated by the synthesis tool. 

In case you deliberately want to implement a combinational loop, write a detailed description of the reason for doing that, and also write a comment in the constraint file. The reason for this last point is due to the fact that the Static Timing Analysis tool (STA) usually increase the minimum period of the system when it founds a combinational loop. Therefore, in this case you should tell to the STA tool to 'ignore' that particular path. The syntax for ignoring a path is 'set_false_path' for the Quartus (Altera) software, and for the ISE (Xilinx) you should use TIG with its resepctivs syntax in both cases.

Get free daily email updates!

Follow us!

Digital Logic in Analog Block - How To Test It?

Analog IP blocks these days have increasing amounts of digital control logic. With very small amounts of digital logic, it's possible to just draw gates on the schematic and run targeted tests that will hopefully catch any errors. But when you have several thousand digital gates, a new approach is needed, as I discovered in a recent discussion.

"2,000 gates is probably a good transition point where people switch from manually inserting gates in a schematic to synthesis," said Bob Melchiorre, director of field operations for digital implementation at Cadence. "Beyond 2,000 gates you have to start thinking about how you're going to test it, because you cannot guarantee that simulation or targeted testing will catch all the issues. Around 10,000 gates it starts getting completely unbearable, and you cannot write enough targeted tests to find all the faults in your digital logic."

Click here to read more ...

Get free daily email updates!

Follow us!

Draw AND gate using XOR gates only

Hi friends….

Do any one know how to design an AND gate using XOR gate.?

This was a good question for discussion among me and my friends during graduation. At last solution was quite impressive. I thought i would be good to discuss it here also as I had found this question is interviews for freshers.

Please let us know your comments and views.

Is it really possible to design AND gate using XOR gate.?
If yes, then HOW?
If no, then WHY?

Get free daily email updates!

Follow us!

Asynchronous Integrated Circuits Design

Many modern integrated circuits are sequenced based on globally distributed periodic timing signals called clocks. This method of sequencing, synchronous, is prevalent and has contributed to the remarkable advancements in the semiconductor industry in form of chip density and speed in the last decades. For the trend to continue as proposed in Moore’s law, the number of transistors on a chip doubles about every two years, there are increasing requirements for enormous circuit complexity and transistor down scaling.

As the industry pursues these factors, many problems associated with switching delay, complexity management and clock distribution have placed limitation on the performance of synchronous system with an acceptable level of reliability. Consequently, the synchronous system design is challenged on foreseeable progress in device technology.

These concerns and other factors have caused resurgence in interest in the design of asynchronous or self-timed circuits that achieve sequencing without global clocks. Instead, synchronization among circuit elements is achieved through local handshakes based on generation and detection of request and acknowledgement signals.

Some notable advantages of asynchronous circuits over their synchronous counterparts are presented below:

* Average case performance. Synchronous circuits have to wait until all possible computations have completed before producing the results, thereby yielding the worst-case performance. In the asynchronous circuits, the system senses when computation has completed thereby enabling average case performance. For circuits like ripple carry adders with significantly worst-case delay than average-case delay, this can be an enormous saving in time.

* Design flexibility and cost reduction, with higher level logic design separated from lower timing design

* Separation of timing from functional correctness in certain types of asynchronous design styles thereby enabling insensitivity to delay variance in layout design, fabrication process, and operating environments.

* The asynchronous circuits consume less power than synchronous since signal transitions occur only in areas involved in current computation.

* The problem of clock skew evident in synchronous circuit is eliminated in the asynchronous circuit since there is no global clock to distribute. The clock skew, difference in arrival times of clock signal at different parts of the circuit, is one of the major problems in the synchronous design as feature size of transistors continues to decrease.

Asynchronous circuit design is not entirely new in theory and practice. It has been studied since the early 1940′s when the focus was mainly on mechanical relays and vacuum tube technologies. These studies resulted to two major theoretical models (Huffman and Muller models) in the 1950′s. Since then, the field of asynchronous circuits went through a number of high interest cycles with a huge amount of work accumulated. However, problems of switching hazards and ordering of operations encountered in early complex asynchronous circuits resulted to its replacement by synchronous circuits. Since then, the synchronous design has emerged as the prevalent design style with nearly all the third (and subsequent) generation computers based on synchronous system timing.

Despite the present unpopularity of the asynchronous circuits in the mainstream commercial chip production and some problems noted above, asynchronous design is an important research area. It promises at least with the combination of synchronous circuits to drive the next generation chip architecture that would achieve highly dependable, ultrahigh-performance computing in the 21st century.

The design of the asynchronous circuit follows the established hardware design flow, which involves in order: system specification, system design, circuit design, layout, verification, fabrication and testing though with major differences in concept. A notable one is the impractical nature of designing an asynchronous system based on ad-hoc fashion. With the use of clocks as in synchronous systems, lesser emphasis is placed on the dynamic state of the circuit whereas the asynchronous designer has to worry over hazard and ordering of operations. This makes it impossible to use the same design techniques applied in synchronous design to asynchronous design.

The design of asynchronous circuit begins with some assumption about gate and wire delay. It is very important that the chip designer examines and validates the assumption for the device technology, the fabrication process, and the operating environment that may impact on the system’s delay distribution throughout its lifetime. Based on this delay assumption, many theoretical models of asynchronous circuits have been identified.

There is the delay-insensitive model in which the correct operation of a circuit is independent of the delays in gates and in the wires connecting the gate, assuming that the delays are finite and positive. The speed-independent model developed by D.E. Muller assumes that gate delays are finite but unbounded, while there is no delay in wires. Another is the Huffman model, which assumes that the gate and wire delays are bounded and the upper bound is known.

For many practical circuit designs, these models are limited. For the examples in this discussion, quasi delay insensitive (QDI), which is a combination of the delay insensitive assumption and isochronic-fork assumption, is used. The latter is an assumption that the relative delay between two wires is less than the delay through a sequence of gates. It assumes that gates have arbitrary delay, and only makes relative timing assumptions on the propagation delay of some signals that fan-out to multiple gates.

Over the years, researchers have developed a method for the synthesis of asynchronous circuits whose correct functioning do not depend on the delays of gates and which permitted multiple concurrent switching signals. The VLSI computations are modeled using Communicating Hardware Processes (CHP) programs that describe their behavior algorithmically. The QDI circuits are synthesized from these programs using semantics-preserving transformations.

In conclusion, as the trend continues to build highly dependable, ultrahigh-performance computing in the 21st century, the asynchronous design promises to play a dominant role.

Dual Edge D-FlipFlop

One important design rule is to use only one edge of the clock signal. Although this is a good design practice in some special cases it might be helpful to use both edges.

Fig. 1

Listing 1. not synthesizable dual-edge behavior in VHDL

process (reset, clock)
begin
if (reset =  ‘1’) then
−− reset
elsif rising_edge(clock) then
−− synchronous behavior
elsif falling_edge (clock) then
−− synchronous behavior
end if;
end process;

One example is low-power signal processing, where all state machines should run at the symbol frequency to avoid unnecessary switching. But the signal frequency might be higher than the symbol frequency.
FM0 encoding (fig. 1) is an example. With FM0 encoding always the signal switches at the begin of every symbol. Another signal switch is done in the middle of the symbol, if zero has to be transmitted. If a transmitter wants so send a FM0 encoded data stream and runs only at the symbol frequency, the output signal has to be switched with the rising edge of clock and additionally with the falling edge, if zero is transmitted.

Another example for dual-edge behavior are clock dividers. For odd divisors the divided clock signal has to be switched at the falling edge of the fast clock, to get the same length for the low and the high period.

There are two problems if dual-edge behavior is desired:

1. Most cell libraries do not provide a dual-edge flip-flops.
2. In VHDL dual-edge behavior can be described as shown in listing 1, but most synthesis tools do not support this. Only few are capable of handling such a description. Therefore we need another way to model dual-edge behavior.

Although dual-edge behavior is not supported by VHDL, synthesis and the cell libraries, a dual-edge flipflop can be described as shown in fig. 2. Note that synthesis tools will transform the multiplexers into XOR gates.

Fig. 2. Pseudo Dual-Edge D-Flipflop (pde dff)

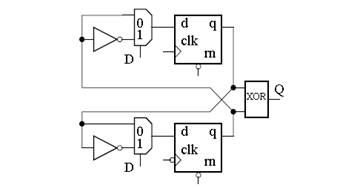
The pde dff consists of 2 cross-coupled flipflops, one triggered by the rising and the other one triggered by the falling edge of the clock signal c. The outputs of the flipflops are connected via an XOR gate. Although not shown in fig. 2, asynchronous set and reset are possible.

The synthesizable VHDL source code of the pde dff is shown in listing 2. Both asynchronous set (sn) and reset (rn) can be turned on or off using generic parameters. Using both edges of the clock means doubling the clock frequency. Propagation paths have to be half as long for dualedge logic compared to common single-edge logic.

Although the pde dff looks symmetric it has in general asymmetric behavior in terms of the propagation time for the rising and the falling edge of the data output q. It depends on the data input d, the stored values in the two flip-flops and the propagation times of both the flip-flops and the final XOR gate.

For the example of FM0 encoding (fig. 1) this means that for a continuous transmission of the symbol zero in general the time of the output q being high is not equal to the time of the output being low. Such an asymmetry is not uncommon even for single-edge flipflops but for the pde dff it is slightly bigger.

Listing2. The Pseudo Dual-Edge D-FF in VHDL:

library IEEE;
use IEEE.STD_LOGIC_1164.ALL;
IEEE.Numeric_std.ALL;

entity pdedff is
generic (
impl_rn: integer := 1; −− with async reset if 1
impl_sn: integer := 1); −− with async set if 1
port(
rn:in std_ulogic; −− low−active
sn:in std_ulogic; −− low−active
d:in std_ulogic;
c:in std_ulogic;
q:out std_ulogic);
end pdedff;

−−pseudo dual−edgeD−flipflop
−−reset and set are lowactive and can be
−−(de)activated using the generic paramters

architecture behavior of pdedff is
signal ff_rise, ff_fall:std_ulogic;
begin

process(rn, sn, c)
begin
if(impl_rn=1 AND rn=’0’) then
ff_rise <= ’0’;
elsif (impl_sn=1 AND sn=’0’) then
ff_rise <= ‘1’;
elsif rising_edge (c) then
if (d= ‘1’) then
ff_rise <= NOT (ff_fall);
else ff_rise <= ff_fall;
endif;
endif;
end process;

process(rn, sn, c)
begin
if(impl_rn = 1 AND rn= ‘0’) then
ff_fall <= ‘0’;
elsif (impl_sn= 1 AND sn = ‘0’) then
ff_fall <= ‘0’;
elsif falling_edge (c) then
if (d = ‘1’) then
ff_fall <= NOT (ff_rise);
else
fffall <= ff_rise;
endif;
endif;
end process;

q <= ‘0’ when (impl_rn = 1 AND rn= ‘0’) else
        ‘1’ when (impl_sn= 1 AND sn= ‘0’) else
        ff_rise XOR ff_fall;
−−rn and sn used to suppress spikes
endbehavior;

Draw AND gate using 2x1 MULTIPLEXER

Look at the truth table of AND gate. When any of the one input is zero output is always zero (or same as that input); when the other input is one, output is dependent on the other input and is same as the other input. Using this property we can draw AND gate in four different ways using 2:1 MUX as shown in the above figure.

Similar concept can be applied to create all basic gates from 2:1 MUX. I will publish all these in coming blog posts along with the elaborated

Get free daily email updates!

Follow us!

Boolean Algebra Simplified

Once one has defined a notation for an algebra, the rules to manipulate expressions follow. The most simple are the rules that concern the unary operator NOT:

(A')' = A

A • A' = 0

A + A' = 1

 

General rules like the distributive, commutative, and associative rules hold for the AND and OR binary operators (except one weird one) so that:

Distributive:

A•(B+C) = A•B + A•C

A+(B•C) = (A+B)•(A+C) (the weird one!)

 

Commutative:

A•B = B•A

A+B = B+A

Associative: (A•B)•C = A•(B•C)

(A+B)+C = A+(B+C)

 

In addition, there are simplification rules for Boolean equations. There are three important groups of simplification rules.

The first one uses just one variable:

A•A = A

A+A = A

 

The second group uses Boolean constants 0 and 1:

A • 0 = 0

A • 1 = A

A + 0 = A

A + 1 = 1

 

The third group involves two or more variables and contains a large number of possible simplification rules (or theorems) such as:

 

A + A•( B ) = A

( proof: A + A•B = A•(1+B) = A•1 = A )

 

Note that in this expression either A or B may stand for any complex Boolean expression.

There are two important rules which constitute de Morgan's theorem:

(A+B)' = A' • B'

(A•B)' = A' + B'

 

This theorem is widely used in Boolean logic design. Stated in words it is: To "invert" (negate) a Boolean expression, you replace the AND operator with the OR operator (or vice versa) and invert the individual terms. The theorem holds for any number of terms, so:

 

(A+B+C)' = ( (A+B)+C)' = ( (A+B)' )•C' = A'•B'•C'

and similarly:

(A•B•C•....•X)' = A' + B' + C' + ......+ X'

 

You may have noticed by now that rules are often given in pairs. It makes sense that in a binary system there is some kind of symmetry between the two operators. For Boolean algebra this symmetry is called Duality. Every equation has its dual which one can generate by replacing the AND operators with ORs (and vice versa) and the constants 0 with 1s (and vice versa).

 

For example, the dual equation of the important simplifying rule:

A + A•B = A

is:

A•(A+B) = A (proof: A•A + A•B = A + A•B = A )

 

Do not mix up or get confused between a dual expression which is generated by the above rules and the complement (or inverted) expression which is generated by applying the NOT operator. The rules are similar, but they mean very different things.

 

Finally, let us consider the proposition (I am not taking an umbrella), or:

 

(U)' = ( C'•(W+R) )'

Apply de Morgan's theorem

U' = (C')' + (W+R)'

Apply de Morgan's theorem again

U' = (C')' + W'•R'

And simplify

U' = C + W'•R'

Cyclic Redundancy Checking (CRC)

Error detection is an important part of communication systems when there is a chance of data getting corrupted. Whether it’s a piece of stored code or a data transmission, you can add a piece of redundant information to validate the data and protect it against corruption. Cyclic redundancy checking is a robust error-checking algorithm, which is commonly used to detect errors either in data transmission or data storage. In this multipart article we explain a few basic principles.

Modulo two arithmetic is simple single-bit binary arithmetic with all carries or borrows ignored. Each digit is considered independently. This article talks about how modulo two addition is equivalent to modulo two subtraction, and can be performed using an exclusive OR operation followed by a brief on Polynomial division where remainder forms the CRC checksum.
For example, we can add two binary numbers X and Y as follows:

10101001 (X) + 00111010 (Y) = 10010011 (Z)

From this example the modulo two addition is equivalent to an exclusive OR operation. What is less obvious is that modulo two subtraction gives the same results as an addition.
From the previous example let’s add X and Z:

10101001 (X) + 10010011 (Z) = 00111010 (Y)

In our previous example we have seen how X + Y = Z therefore Y = Z – X, but the example above shows that Z+X = Y also, hence modulo two addition is equivalent to modulo two subtraction, and can be performed using an exclusive OR operation.

In integer division dividing A by B will result in a quotient Q, and a remainder R. Polynomial division is similar except that when A and B are polynomials, the remainder is a polynomial, whose degree is less than B.

The key point here is that any change to the polynomial A causes a change to the remainder R. This behavior forms the basis of the cyclic redundancy checking.
If we consider a polynomial, whose coefficients are zeros and ones (modulo two), this polynomial can be easily represented by its coefficients as binary powers of two.

In terms of cyclic redundancy calculations, the polynomial A would be the binary message string or data and polynomial B would be the generator polynomial. The remainder R would be the cyclic redundancy checksum. If the data changed or became corrupt, then a different remainder would be calculated.

Although the algorithm for cyclic redundancy calculations looks complicated, it only involves shifting and exclusive OR operations. Using modulo two arithmetic, division is just a shift operation and subtraction is an exclusive OR operation.

Cyclic redundancy calculations can therefore be efficiently implemented in hardware, using a shift register modified with XOR gates. The shift register should have the same number of bits as the degree of the generator polynomial and an XOR gate at each bit, where the generator polynomial coefficient is one.

Augmentation is a technique used to produce a null CRC result, while preserving both the original data and the CRC checksum. In communication systems using cyclic redundancy checking, it would be desirable to obtain a null CRC result for each transmission, as the simplified verification will help to speed up the data handling.

Traditionally, a null CRC result is generated by adding the cyclic redundancy checksum to the data, and calculating the CRC on the new data. While this simplifies the verification, it has the unfortunate side effect of changing the data. Any node receiving the data+CRC result will be able to verify that no corruption has occurred, but will be unable to extract the original data, because the checksum is not known. This can be overcome by transmitting the checksum along with the modified data, but any data-handling advantage gained in the verification process is offset by the additional steps needed to recover the original data.

Augmentation allows the data to be transmitted along with its checksum, and still obtain a null CRC result. As explained before when obtain a null CRC result, the data changes, when the checksum is added. Augmentation avoids this by shifting the data left or augmenting it with a number of zeros, equivalent to the degree of the generator polynomial. When the CRC result for the shifted data is added, both the original data and the checksum are preserved.

In this example, our generator polynomial (x3 + x2 + 1 or 1101) is of degree 3, so the data (0xD6B5) is shifted to the left by three places or augmented by three zeros.

0xD6B5 = 1101011010110101 becomes 0x6B5A8 = 1101011010110101000.

Note that the original data is still present within the augmented data.
0x6B5A8 = 1101011010110101000
Data = D6B5 Augmentation = 000

Calculating the CRC result for the augmented data (0x6B5A8) using our generator polynomial (1101), gives a remainder of 101 (degree 2). If we add this to the augmented data, we get:

0x6B5A8 + 0b101 = 1101011010110101000 + 101
= 1101011010110101101
= 0x6B5AD

As discussed before, calculating the cyclic redundancy checksum for 0x6B5AD will result in a null checksum, simplifying the verification. What is less apparent is that the original data is still preserved intact.

0x6B5AD = 1101011010110101101
Data = D6B5 CRC = 101

The degree of the remainder or cyclic redundancy checksum is always less than the degree of the generator polynomial. By augmenting the data with a number of zeros equivalent to the degree of the generator polynomial, we ensure that the addition of the checksum does not affect the augmented data.

In any communications system using cyclic redundancy checking, the same generator polynomial will be used by both transmitting and receiving nodes to generate checksums and verify data. As the receiving node knows the degree of the generator polynomial, it is a simple task for it to verify the transmission by calculating the checksum and testing for zero, and then extract the data by discarding the last three bits.

Thus augmentation preserves the data, while allowing a null cyclic redundancy checksum for faster verification and data handling.

Edge triggered D Flip Flop

Below figure shows the Diagram of Edge triggered d flip flop

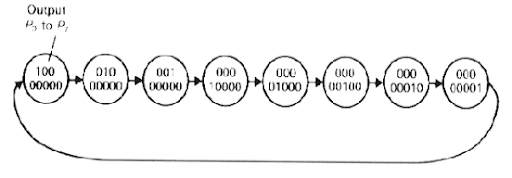
Johnson Counter

The Johnson counter, also called the twisted ring counter, is a variation of the ring counter, with the inverse output of the most significant flip-flop passed to the input of the least significant flip-flop. The sequence followed begins with all 0's in the register. The final 0 will cause 1's to be shifted into the register from the left-hand side when clock pulses are applied. When the first 1 reaches the most significant flip-flop, 0's will be inserted into the first flip-flop because of the cross-coupling between the output and the input of the counter.

Links:

• Different type of counters
• Binary counters
• Up/down counters
• Loadable counters
• BCD Counter
• Ring counters

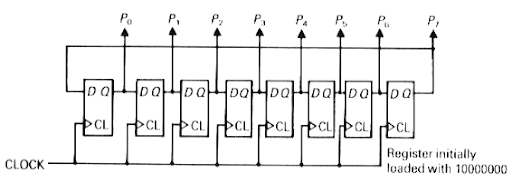
Ring counter

A ring counter is a circular shift register with only one flip-flop being set at any particular time; all others are cleared. The single bit is shifted from one flip-flop to the other to produce the sequence of timing signals.

Links:

• Different type of counters
• Binary counters
• Up/down counters
• Loadable counters
• BCD Counter
• Johnson counters

BCD Counter

A BCD counter counts in binary-coded decimal from 0000 to 1001 and back to 0000. Because of the return to 0 after a count of 9, a BCD counter does not have a regular pattern as in a straight binary count.

Links:

• Different type of counters
• Binary counters
• Up/down counters
• Loadable counters 

• Ring Counter
• Johnson counters

How are counters made?

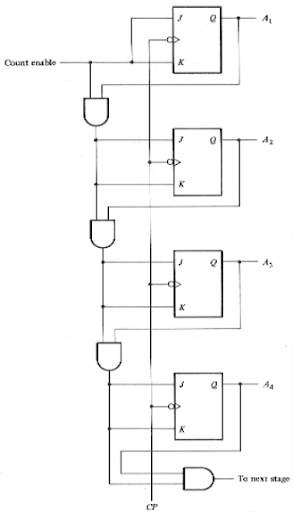
Counters are generally made up of flip-flops and logic gates. Like flip-flops, counters can retain an output state after the input condition which brought about that state has been removed. Consequently, digital counters are classified as sequential circuits. While a flip-flop can occupy one of only two possible sattes, a counter can have many more than two states. In the case of a counter, the value of a state is expressed as a multidigit binary number, whose `1's and `0's are usually derived from the outputs of internal flip-flops that make up the counter. The number of states a counter may have is limited only by the amount of electronic hardware that is available. The main types of flip-flops used are J-K flip-flops or T flip-flops, which are J-K flip-flops with both J and K inputs tied together. Before that, here's a quick reminder of how a J-K flip-flop works:

J input	K input	Output, Q
0	0	Q
0	1	0
1	0	1
1	1	not Q

T flip-flops are used because set/reset ([1,0] [0,1]) functions are seldom used. Only the "do nothing" and toggle ([0,0] [1,1]) functions are used. Logic gates are used to decide when to toggle which outputs. Below is an example of a synchronous binary counter, implemented using J-K flip-flops and AND gates.

Read More

• Why do we need counters?

• Synchronous Counter

• Why “Synchronous”?

• Different type of counters

Get free daily email updates!

Follow us!